Curves & Lines
Math
Imaginary math
Trigonometry
Calculus
Area & Volume
Line
Slope intercept
y = mx + k
m is slope, Δy/Δx
Point-slope form
y – y₁ = m(x – x₁)
Two points form
y – y₁ = (x – x₁)(y₂ – y₁) / (x₂ – x₁)
Intercept form
(x/a) + (y/b) = 1
a is x intercept
b is y intercept
Standard Form: the standard form of a line is in the form
Ax + By = C where A is a positive integer, and B, and C are integers.
Two lines are perpendicular if the product of their slopes is −1
or one has a slope of 0 (a horizontal line) and the other has an
undefined slope (a vertical line).
distance between two points
d = √(Δx² + Δy² + Δz²)
Distance point to line
line is ax + by + c = 0
point is x₀, y₀
distance is |ax₀ + by₀ + c| / √(a² + b²)
Angles
Complementary angles add up to 90º or π/2
Supplimentary angles add up to 180º or π
explementary angles add up to 360º or 2π
acute angles are <90º
right angle is 90º
obtuse angles are >90º and <180º
straight angle is 180º
oblique angles are those not n•90º
Circle
equation of circle with center at a,b and radius r
(x–a)² + (y–b)² = r²
center at the origin
x² + y² = r²
three point form of a circle is:
[ (x–x₁)(x–x₂) + (y–y₁)(y–y₂) ] / [ (y–y₁)(x–x₂) – (y–y₂)(x–x₁) ] =
[(x₃–x₁)(x₃–x₂) + (y₃–y₁)(y₃–y₂)] / [(y₃–y₁)(x₃–x₂) – (y₃–y₂)(x₃–x₁)]
A = πr²
length of chord
L = 2√(r²-d²)
r = radius
d = perpendicular distance from chord to center
Area of a segment
A = (r²/2)[(π/180)θ – sinθ]
Plane
General equation of a plane: ax + by + cz + d = 0
if d=0, plane goes thru the origin
if x₀ y₀ z₀ are where plane intersects the 3 axes...
x₀a = y₀b = z₀c = –d
use this to solve for a,b,c,d
sphere
equation of sphere with center at a,b,c and radius r
(x–a)² + (y–b)² + (z–c)² = r²
center at the origin
x² + y² + z² = r²
The equation of the sphere centred at (x₀,y₀,z₀) and
passing through (x₁,y₁,z₁) is
(x-x₀)²+(y-y₀)²+(z-z₀)² = (x₁-x₀)²+(y₁-y₀)²+(z₁-z₀)²
Parabola
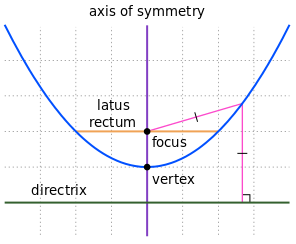
Parabola vertical
4p(y–k) = (x–h)²
p is distance
vertex to focus,
if positive opens up
p is also distance
vertex to directorix
vertex at (h, k)
Parabola open sideways
4p(x–h) = (y–k)²
p is distance
vertex to focus,
if positive opens
to the right
p is also distance
vertex to directorix
vertex at (h, k)
Ellipse
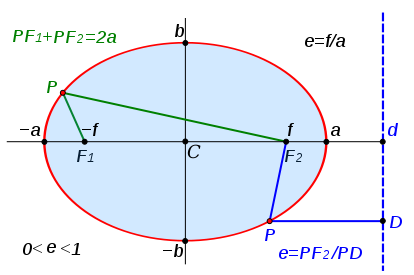
The area is πab
where a and b are one-half of the ellipse's major and minor axes
and are the vertices. F₁ and F₂. The sum of the distances from any point P
on the ellipse to those two foci is constant and equal to the major axis
(PF₁ + PF₂ = 2a)
foci are at a distance c from origin along the x axis, where c² = a² – b²
Ellipse whose axis correspond to the x and y axis has the equation
(x/a)² + (y/b)² = 1
a & b are distance from origin to curve along x or y axis.
Ellipse centered at x₁ and y₁, the equation is
((x – x₁)/a)² + ((y – y₁)/b)² = 1
a & b are distance from center to curve along x or y axis.
Hyperbola
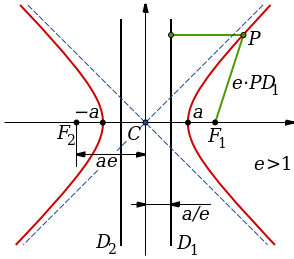
The hyperbola consists of the red curves. The asymptotes of the
hyperbola are shown as blue dashed lines and intersect at the center
of the hyperbola, C. The two focal points are labeled F1 and F2, and
the thin black line joining them is the transverse axis. The
perpendicular thin black line through the center is the conjugate
axis. The two thick black lines parallel to the conjugate axis (thus,
perpendicular to the transverse axis) are the two directrices, D1 and
D2. The eccentricity e equals the ratio of the distances from a point
P on the hyperbola to one focus and its corresponding directrix line
(shown in green). The two vertices are located on the transverse axis
at ±a relative to the center. So the parameters are:
a — distance from center C to either vertex
b — length of a segment perpendicular to the transverse axis drawn
from each vertex to the asymptotes
c — distance from center C to either Focus point, F1 and F2, and
θ — angle formed by each asymptote with the transverse axis.
The shape of a hyperbola is defined entirely by its eccentricity ε,
which is a dimensionless number always greater than one. The distance
c from the center to the foci equals aε. The eccentricity can also be
defined as the ratio of the distances to either focus and to a
corresponding line known as the directrix; hence, the distance from
the center to the directrices equals a/ε. In terms of the parameters
a, b, c and the angle θ, the eccentricity ε equals
ε = c/a = √(1 + (b²/a²)) = secθ
For example, the eccentricity ε of a rectangular hyperbola
(θ = 45°, a = b) equals √2.
East-West opening hyperbola, ie,
the transverse axis of any hyperbola is aligned with the x-axis
and is centered on the origin
(x²/a²) – (y²/b²) = 1
North–South opening hyperbola, ie,
the transverse axis of any hyperbola is aligned with the y-axis
and is centered on the origin
(y²/a²) – (x²/b²) = 1
Area, Volume
Atomic Mass
Black Body Radiation
Boolean Algebra
Calculus
Capacitor
Center of Mass
Carnot Cycle
Charge
Chemistry
Elements
Reactions
Circuits
Complex numbers
Constants
Curves, lines
deciBell
Density
Electronics
Elements
Flow in fluids
Fourier's Law
Gases
Gravitation
Greek Alphabet
Horizon Distance
Interest
Magnetics
Math Trig
Math, complex
Maxwell's Eq's
Motion
Newton's Laws
Octal/Hex Codes
Orbital Mechanics
Particles
Parts, Analog IC
Digital IC Discrete
Pendulum
Planets
Pressure
Prime Numbers
Questions
Radiation
Refraction
Relativistic Motion
Resistance, Resistivity
Rotation
Series
SI (metric) prefixes
Skin Effect
Specific Heat
Springs
Stellar magnitude
Thermal
Thermal Conductivity
Thermal Expansion
Thermodynamics
Trigonometry
Units, Conversions
Vectors
Volume, Area
Water
Wave Motion
Wire, Cu Al metric
Young's Modulus