Circuits
Circuits   electronics   resistors   capacitors

Resistor Networks

Series resistors
Rt = R₁ + R₂ + R₃ + ...
Parallel resistors
1/Rt = (1/R₁) + (1/R₂) + (1/R₃) + ...
Rt = R₁R₂ / (R₁+R₂)

Current divider
N resistors in parallel with current flowing into the junction
Ix = If•Rt / (Rx+Rt)
Rt is total resistance excluding Rx
Ix is current in branch with Rx
It is total current into the node

Voltage divider
2 resistors in Series with voltage V applied to the pair.
Voltage across R₁:
V₁ = V(R₁) / (R₁ + R₂)

Delta-Wye transformations
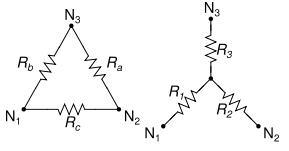
Delta to Wye
R₁ = (RbRc) / (Ra+Rb+Rc)
R₂ = (RaRc) / (Ra+Rb+Rc)
R₃ = (RaRb) / (Ra+Rb+Rc)

Wye to Delta
Ra = (R₁R₂+R₂R₃+R₁R₃)/R₁
Rb = (R₁R₂+R₂R₃+R₁R₃)/R₂
Rc = (R₁R₂+R₂R₃+R₁R₃)/R₃

Millman's theorem
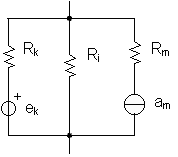
For a circuit consisting of simple branches in parallel.
It provides the voltage across all the parallel branches.
Let Vk be the voltage generators and Am the current generators.
Let Ri be the R's on the branches with no generator.
Let Rk be the R's on the branches with voltage generators.
Let Rm be the R's on the branches with current generators.
The voltage at the ends of the circuit is given by:
V = [ Σ(Vk/Rk) + ΣAm ] / [ Σ(1/Rk) + Σ(1/Ri) ]

Ohm's Law
R is resistance in ohms, E is voltage in volts,
   I is current in amps
E = IR    I = E/R    R = E/I The superposition theorem for electrical circuits states that for a linear system the response (voltage or current) in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, where all the other independent sources are replaced by their internal impedances.

Capacitor Networks
Parallel capacitors
Ct = C₁ + C₂ + C₃ + ...
Series capacitors
1/Ct = (1/C₁) + (1/C₂) + (1/C₃) + ...

L/C

Capacitor: current leads the voltage or voltage lags the current
inductor: current lags the voltage or voltage leads the current

resonance, series
   f = 1/(2π√(LC))
   ω = 1/(√(LC))
   Q = X/R, where X is either Xʟ or Xc
   Q = f/Δf, f=resonant f, and Δf = bandwidth

For a series circuit of a resistor R, a capacitor C and
an inductor L, the impedance may be calculated as follows:
Capacitive Reactance Xc = 1/(2πfC) = 1/ωC
Inductive Reactance Xʟ = 2πfL = ωL
Impedance Z = √(R² + X²)
where X = Xʟ – Xc
ω = 2πf
Phase angle θ = arctan (X/R)
Xc, Xʟ, Z are in Ω, f is in Hz
C in farads, L in Henrys

I = E/Z at angle θ
Vc = I*Xc laging the current by 90º
Vʟ = I*Xʟ leading the current by 90º
Vr = I*R in phase with current

Rectifier and filters
voltage out of FW rectifier, no cap =
VDC = VAC x 1.414 x 2/π = 0.90 VAC (RMS)
Half wave is half that or 0.45 VAC (RMS)

Capacitor input filter, full wave
Ripple voltage p-p = IT/C
V(RMS) is (0.29)(IT/C)
T = 8ms for 60Hz. I is load current

Sine Wave
y(t) = A•sin(2πft + Φ) = A•sin(ωt + Φ)
A is amplitude (peak value)
f is frequency in Hz
t is time in seconds
ω = 2πf is angular frequency in radians / second
Φ is phase in radians

120 volts 60 Hz mains
y = 170 sin 377t

Power
There are three kinds of power
   • real or resistive power (the only one that results in heat)
   • reactive power
   • total power S, or apparent power, the vector sum of the above two, or the product of the RMS voltage and the RMS current
  θ is the phase angle between the current and voltage
  real power P = S cos θ

P = E*I
P = E²/R
P = I²R
1HP = 746 watts
1 amp = 1 coulomb per second = 6.242e18 electrons per sec

AC Power
Real power (P) or active power[1]: watt [W]
Reactive power (Q): volt-ampere reactive [var]
Complex power (S): volt-ampere [VA] or apparent power
Apparent Power (|S|), that is, the absolute value of complex power S: volt-ampere [VA]
Phase of Voltage Relative to Current (φ), the angle of difference (in degrees) between voltage and current;
Current lagging Voltage (Quadrant I Vector), Current leading voltage (Quadrant IV Vector)
Power Factor (PF) The ratio of real power to apparent power and is a dimensionless number between 0 and 1.

The product of voltage and current is the apparent power in AC circuits. It does not take into account that some of the apparent power can be reactive current due to inductors or capacitors. If the load is truly resistive, the true and apparent power are the same, and the power factor is 1.
True_power = apparent_power * power_factor (of the load)

True power is important because that relates to the mechanical power driving the generator, or produced by a motor. Apparent power is important too, as it causes extra current to flow in windings and cables, which must be considered.

Generally the power factor is not always known but can be estimated, taken from the nameplate of a motor, or taken as a worst case of perhaps 0.8. Power factor is the ratio of true power to apparent power, which is cos (theta) where theta is the angle between the voltage and current (this is a sine wave situation). Therefore measuring the current to voltage phase angle can be used to find the power factor. A true watt meter uses an approach along these lines.

Single phase power is generally provided and calculated by the line to neutral voltage, which is 230V in most of the world. The line to line voltage is sqrt(3) * phase to neutral voltage, around 400V for 230V systems, or 415V for a 240V system. To calculate power in such a system, use the line to neutral voltage always, even if the connection is line to line. Thus 230V or 240V * current in each line gives apparent power for each line. Correct for power factor. Then add the three powers.

Shockley diode equation
I = Is(e^(Vd/nVt) – 1)
I is diode current
Is is reverse bias saturation current
Vd is voltage across the diode
Vt is the thermal voltage, 25.85 mV at 300 K
n is a quality factor, usually =1

for n=1, we get the ideal diode equation
Vt = kT/q
k is Boltzmann constant, 1.381e-23 J/K
T is temperature of junction in kelvins
q is charge on an electron 1.602e-19 C

drift velocity Vd
Vd = I / nqA
   Vd is drift velocity in m/s
   I is current
   n is the number of charge carriers per m³
   for copper, 8.5e28 electrons per m³.
   A = πr² is the cross sectional area in m²
   q is the charge of the charge carriers (electrons)
   q = –1.602e-19 Coulomb (charge on an electron)